47
INTERNATIONAL
ANDSPECIALIZED TRANSPORT
■
MARCH 2015
assumptions.Not all behavioural issues are
the result ofwilfulwrongdoingbut could
be the result of simplynot knowing. The
laws of nature, however, always apply and
areunforgiving.
TheFEM
5.016
guidancepaper that
Jansen andMeissner refer to is apaper that
everydirector, salesmanager, supervisor
and craneoperator should read to
understandhowwind can affect a crane
while erectingwind turbines and that
underestimatingorneglectingwind isno
laughingmatter.
In this article the intention is togive
somemorebackground information to
aid in theunderstandingwhy liftingwind
turbine components isdifferent from
performingother lifts.
The formula abovewaspresented in the
previous article. It calculates theperiod
(T) of a freehanging load such as anacelle.
Theperiod isdefined as one full swing,
i.e. the time it takes for the load to swing
from the far left to the far right andback.
Let’s assume thatwe are lifting anacelle
to a100metre elevation.According to the
formula theperiod (T) of thenacellewhile
at ground level (it has just been liftedoff
the transporter) is 20 seconds.
Once again, the formuladoesnot
take into account theweight (mass) of
thenacellenordoes it take into account
the (initial) amplitude angle.Amplitude
anglebeing the angle thenacelle swings
away from its vertical neutral position.
Both amplitude angle andmasshaveno
influenceon theperiod (T).
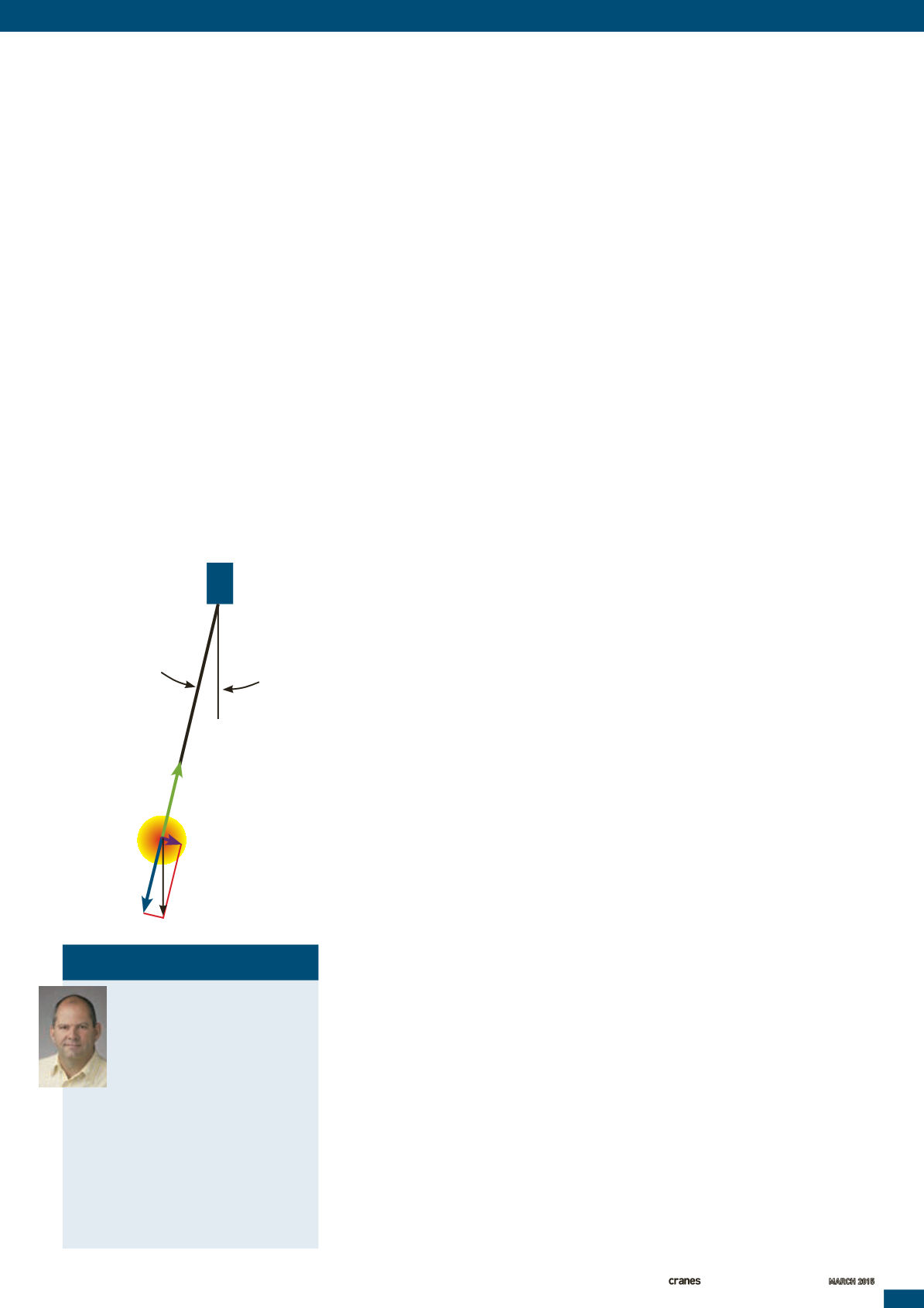
Figure1 shows the forces that play
on a freely suspended load. ThisFigure
is applicable for all suspended loads,
irrespectiveofmass, lengthof rope and
amplitude angle. The (near) horizontal
component (mg sinθ) is the force that is
responsible fordecelerating the load and
bringing it back to itsneutral position
which is vertical. For small angles of θ
(Theta) thishorizontal component is
also the side force that the craneboom is
subjected to. This forcedoesnot just stay at
theboom; it transfers all thewaydown to
ground level and can result in an increase
ingroundpressureunderneath the crane.
Figure2 shows thedifferent stages of
a freely swaying suspended load: pointA
being theneutral vertical point, andpoints
B andCbeing the extremes of theperiod
(T) (withBbeing the left extreme andC
being the right extreme). In eachof these
points the loadpossesses a certain amount
of bothpotential energy andkinetic energy.
Kinetic energy (K.E.) is the energy that
the loadpossessesdue to itsmotion, it is
expressed as:
K.E.=½mv
2
m=mass of the load
V=velocityof the load
Potential energy (P.E.) is the energy that
the loadpossessesdue to its location, it is
expressed as:
P.E.=mgh
m=mass of the load
g=gravity
h=height compared to its initial position
The sumof potential energy andkinetic
energy is calledmechanical energy (M.E.)
Mechanical energy remains constant as
long aswedonot addor take away energy.
K.E. +P.E. =M.E. =constant
Back toFigure 2, if the loadwas
hanging still andperfectly vertical itwould
be inpointA.We therefore call pointA
the initial point or startingpoint.
Let us assume, however, that the load
has just been liftedoff a transporter and it
is slightly swaying from left to right.
When it reaches point B, its velocity
(v) decreases to zero (0) as it is about to
reverse its direction.When the velocity (v)
is zero (0) itmeans that its kinetic energy
is also zero (0). It can, therefore, be stated
that inpoint B the loadonlypossesses
potential energy. This potential energy is
transformed from the kinetic energy and
is equal to “m gh”. Since themass and the
gravity are constant, we can say that the
potential energy (transformed from the
kinetic energy) determines thedifference
inheight (h) compared to its initial point.
Thismakes sense as a faster swaying load
will reach (obviously) higher. The same
applies for pointC.
InpointA, where the loadpossesses no
potential energybut onlykinetic energy,
the velocityof the load is at its highest.
On either side of pointA the velocityof
the loaddecreases until it reaches zero (0)
ABOUTTHEAUTHOR
Marco van Daal has been in
the heavy lift and transport
industry since 1993. He started
at Mammoet Transport from the
Netherlands and later with Fagioli
PSC from Italy, both leading
companies in the industry. His 20-year
plus experience extends to five continents
andmore than 55 countries. It resulted
in a book The Art of Heavy Transport,
available at:
Van Daal has a real passion for sharing
knowledge and experience and holds
seminars around theworld.
THEKNOWLEDGE
Around in theground
MARCOVANDAAL takes a closer look at what goes
on around andunderneath a cranewhen liftingwind
turbine components
T=2π
√
(l/g)
I
t isworthmentioning that thewind
industryhas been subject to ahigher
percentageof crane accidents than
other industries. In the January issueof
IC
, Søren Jansen andKlausMeissner
wrote an excellent articleon the safeuseof
mobile cranes. Theyhighlight that (almost)
all crane accident cases are causedby
behavioural issues as opposed to technical
issues. Behavioural issues cover everything
from theway theoperatorhandles the
crane tohow andwhere the crane is set
up, engineering issues and incorrect
Figure 1
L
mg
cos
Ѳ
Ѳ
mg
cos
Ѳ mg
mg
sin
Ѳ
>


